Eventual Consistency and Conflict Resolution - Part 2
Listen to the Audio Blog
Conflict Resolution using Vector Clocks
The good thing about physical clock timestamps is that they carry information related to the real-time order of events, e.g., if we write v2, one minute after writing v1, the physical timestamp of v2 will be most likely larger than that of v1, assuming we have reasonable clock synchronization in place. However, physical clocks are not 100% accurate. Thus, due to clock synchronization errors, the timestamps may not reflect the true order of events that are too close to each other, e.g. if we write v2 right after writing v1. That inaccuracy may result in unexpected behavior when we have clear causality between updates. For example, when a client first reads the value of a counter as v1 and then writes v2 = v1 + 1 for the counter, v2 depends on v1. Thus, v2 must appear in the order after v1. However, as we saw in the first part (Figure 1), due to the clock skew, we may lose this increment, if we rely on physical timestamps.
On the other hand, the good thing about logical clock timestamps is that they capture causality. However, they are not related to the wall clock time, causing unexpected behavior as well. We saw the root cause of this unexpected behavior is the skew of logical clocks when we have an update frequency mismatch between replicas. Note that the issue of logical clocks happens for concurrent updates, i.e., updates that are NOT causally related to each other. Updates that are causally related to each other are always correctly ordered by logical clocks.
So, let's see: When we have causality between values, logical timestamps are great. On the other hand, when we don't have causal relation between values, physical timestamps work better. Thus, if only we had a way to know if two updates are causally related or not, we could do this:
Given two updates v1 and v2
- If v1 and v2 are causally related, use the causality to order them.
- If v1 and v2 are not causally related, use physical timestamps to order them.
Unfortunately, using Lamport's logical clocks, we can not detect concurrent updates. Specifically, logical clocks only satisfy the following property:
v2 depends on v1 => v1.lc < v2.lc
But to detect concurrent updates, we need timestamps that satisfy the other way as well:
v2 depends on v1 <=> v1.timestamp < v2.timestamp
To have the condition above, we can use Vector Clocks (VCs). VCs are a generalization of Lamport's clocks. Instead of a single integer, we use a vector of integers each representing the local counter of each node. Each replica updates its VC as follows:
- Starts with a vector of counters (one counter per replica, all initially set to 0)
- Before each local update, increment its own counter.
- Whenever received a remote update with vector clock timestamp vc, sets the VC to max(vc, current VC value).
- To take maximum, we take an entry-wise maximum.
Two VC timestamps are ordered as follows:
vc1 < vc2 <=> (∀i vc1[i] <= vc2[i]) AND (∃j vc1[j] < vc2[j])
So basically, for vector timestamp vc2 to be larger than vc1, each entry of vc2 must be greater than or equal to the corresponding entry in vc1, and also at least one of the entries of vc2 must be strictly larger than its corresponding entry in vc1. Note that this order is not a total order, i.e., it is possible neither vc1 < vc2 nor vc2 < vc1. In that case, we say vc1 and vc2 are concurrent and denoted them as vc1 | vc2. Two VC timestamps are equal if all entries are equal.
Now, consider this protocol: We timestamp each update with <vc, pt> where the vc is the value of the vector clock and pt is the value of the physical clock. We define our order as follows:
v1 ≤ v2 iff (v1.vc ≤ v2.vc) OR (v1.vc | v2.vc and v1.pt ≤ v2.pt)
So v1 is before v2 in the order if and only if the value of its vector clock is smaller than that of v2, or if vector clocks are concurrent, the physical timestamp of v1 is smaller than that of v2. If v1 and v2 are equal in order based on this comparison, we use the replica IDs to break the tie. We define our merge function to simply pick one of the given values that is later according to the order defined above, i.e., Merge(v1, v2) = if v1.timestamp < v2.timestamp then v2 else v1. Let's see if this protocol satisfies sufficient conditions for the eventual consistency, explained in the first part.
Condition 1 is satisfied because our order is a proper partial order (we have a total order, but any total order is also a partial order). Condition 2 is satisfied according to the vector clock algorithm and the definition of our order. Specifically, because every time we increase the local counter, the VC of the new update is larger than the VC of the existing version, thus, our updates are monotonically non-decreasing according to our order. Condition 3 is also satisfied because we are picking one of the given versions and the picked version is greater than or equal to each of the given versions, thus it is the LUB of two given versions.
Thus, the conflict resolution using vector clocks explained above satisfies sufficient conditions of eventual consistency. Now, let's see how this protocol avoids the lost update scenario shown in Figure 2 in the first part. When replica B receives v1 from replica A, it updates its vector clock to <1,0>. Before applying the update from the client for v2, it increments its own counter in the VC. The resulting VC timestamp, <1,1> is larger than VC timestamp of v1. Thus, Condition 2 is satisfied. When replica A receives v2, the merge function returns v2 as the winning version. Thus, both replicas consider v2 as the final version and no update is lost.
Using vector clocks for conflict detection is proposed in the original Dynamo paper [1], but as far as I know, it is not the approach used in the actual Amazon DynamoDB today. (Side note: I have covered DynamoDB transactions in this blog. Check out this post, if you are interested)
Conflict Resolution using Hybrid Logical Clocks (HLCs)
The vector clocks are great; using vector clocks we can guarantee eventual consistency while avoiding lost updates, and by falling back to physical clocks in case of concurrent updates, we approximate the real-time order of updates. However, vector clocks are expensive. Bernadette Charron-Bost showed in [2] that to capture causality with N processes, each vector clock timestamp takes O(N) space. That becomes prohibitive when we have a partitioned system with hundreds or thousands of shards. Specifically, if want to let shards of a replica independently write (which is almost always the case), then they should be able to timestamp independently. Thus, according to the Charron-Bost theorem [2], we need to have one entry per shard per replica in our vector clock timestamps. That could be too much metadata overhead.
So for practical systems, vector clocks may not be feasible. Let's take a step back and see if we can fix the issue with physical and logical timestamps, maybe by mixing them!
Can we have timestamps that, while being close to the physical clock, capture causality? This is exactly what Sandeep Kulkarni and Murat Demirbas proposed to do in [3]. They called their clock algorithm Hybrid Logical Clock (HLC) due to its hybrid nature; it is sort of a physical clock because its values are close to the system clock, and at the same time it captures causality like Lamport's logical clock.
An HLC timestamp is a tuple <l, c>. The values for l are coming from the physical clock. The c component is a simple integer counter that is used to capture causality when l does not respect causality (due to the clock skew). Algorithm 1 shows how each replica maintains its HLC. On each local update, the replica updates its HLC and uses the resulting value to timestamp the update. To update the HLC upon a local update, we first read the value of physical clock denoted as pt in the algorithm. We set the l part of the HLC to the maximum of the current l value and pt. If the current l is larger than pt, we know the physical clock on this node is behind. Thus, to capture causality, we increment c. Otherwise, we reset c to 0. This reset mechanism guarantees that c will be bounded assuming we have a clock synchronization that keeps clock skew bounded [3].
Upon receiving a remote update, the receiving replica updates its HLC as well. Each remote update has an HLC timestamp denoted as t in Algorithm 1. We set the value of l to the maximum of the current l value, the l value of the timestamp of the remote update, and the value of the physical clock. Then, we update c, as shown in Algorithm 1.
| Algorithm 1. HLC Algorithm |
|
Local Update old_l = hlc.l hlc.l = max(hlc.l, pt) if (hlc.l = old_l) hlc.c = hlc.c + 1 else hlc.c = 0 Receiving Remote Update (with hlc timestamp t) old_l = hlc.l hlc.l = max(hlc.l, t.l, pt) if (hlc.l = old_l = t.l) c = max(hlc.c, t.c)+1 else if (hlc.l = old.l) c = hlc.c + 1 else if (hlc.l = t.l) c = t.c + 1 else c = 0 |
Just like Lamport's logical clock timestamps, HLC timestamps satisfy the following property:
v2 depends on v1 => v1.hlc < v2.hlc
However, unlike logical clocks, the values of HLCs are close to the physical time. Specifically, the values for l part are coming from the physical clocks.
Two HLC timestamps are compared as follows:
hlc1 < hlc2 <=> (hlc1.l < hlc2.l) OR (hlc1.l = hlc2.l AND hlc1.c < hlc2.c)
Now consider this protocol: Each replica maintains an HLC. The replica uses the value of its HLC to timestamp values that it writes. We define our order based on the timestamps, i.e., a version with a higher HLC timestamp is later in the order than a version with a smaller timestamp. Again, we break the ties according to replica IDs.
Condition 1 and 3 are satisfied similar to LWW with physical timestamps. Since we update HLC when we receive an update from another replica, it is guaranteed that future updates in the receiving replica have a higher timestamp than the remote update. Thus, we avoid the problem with the physical timestamp shown in Figure 1 in the first part, and this protocol satisfies Condition 2 as well.
So this is awesome! using HLC we can provide eventual consistency while avoiding problems of other methods. Specifically,
- We avoid lost updates due to the skew of physical clocks.
- We avoid violation of real-time expectations due to the skew of logical clocks.
- We avoid the overhead of vector clocks.
Several new databases have adopted HLCs [4-7]. These systems use HLCs for slightly different purposes. However, the main reason that they use HLCs is the same which is capturing causality while being close to physical time. Couchbase uses HLCs or conflict resolution for its cross-datacenter replication [5]. Thus, its usage is exactly the approach we discussed in this post. CockroachDB [4] and yugabyteDB [7] are similar to Google Spanner, and use HLCs instead of Spanner TrueTime to have proper versioning for causally related updates. MongoDB uses HLCs to provide causal consistency [6]. Causal consistency is a consistency model stronger than eventual consistency. The nice thing about causal consistency is that a causally consistent system can remain available even in presence of network partition. Thus, CAP does not apply to causal consistency. For that reason, causal consistency is very interesting and is gaining more attention. If you are interested in causal consistency, you can also refer to [8].

|
|
Figure 3. Some of the databases that use HLCs
|
I anticipate more data stores will use HLCs in the future. The thing is, HLC timestamps are superior to both physical and logical timestamps and have no additional overhead. Note that using the compact encoding of HLC proposed in [3], we can encode HLC timestamps in 64-bit integers, just like normal physical timestamps with good enough granularity. Figure 4 summarizes different clocks algorithms that we discussed for conflict resolution.
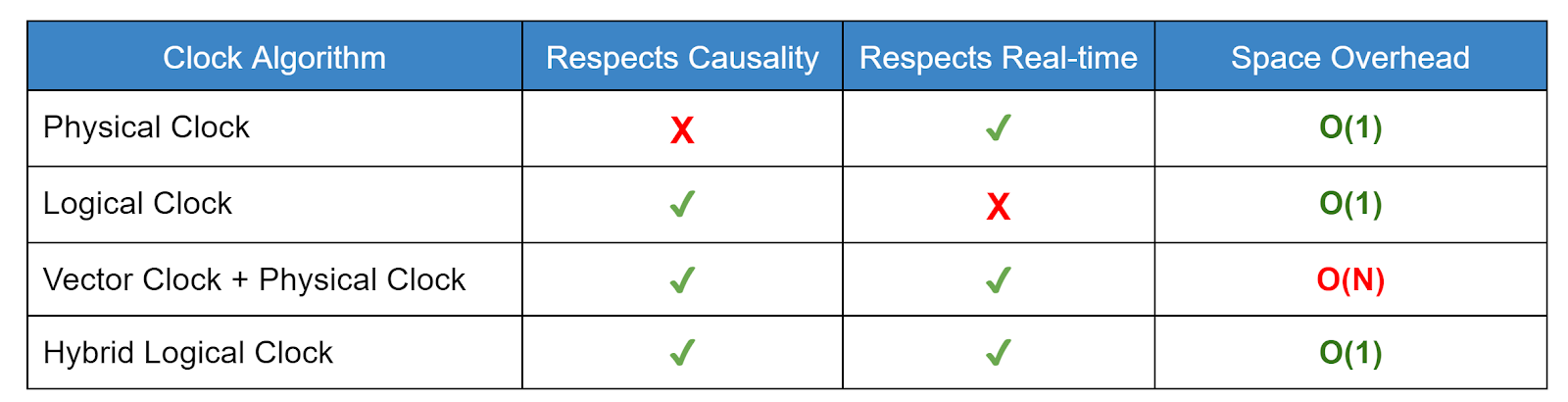
|
|
|






Comments
Post a Comment